Publications

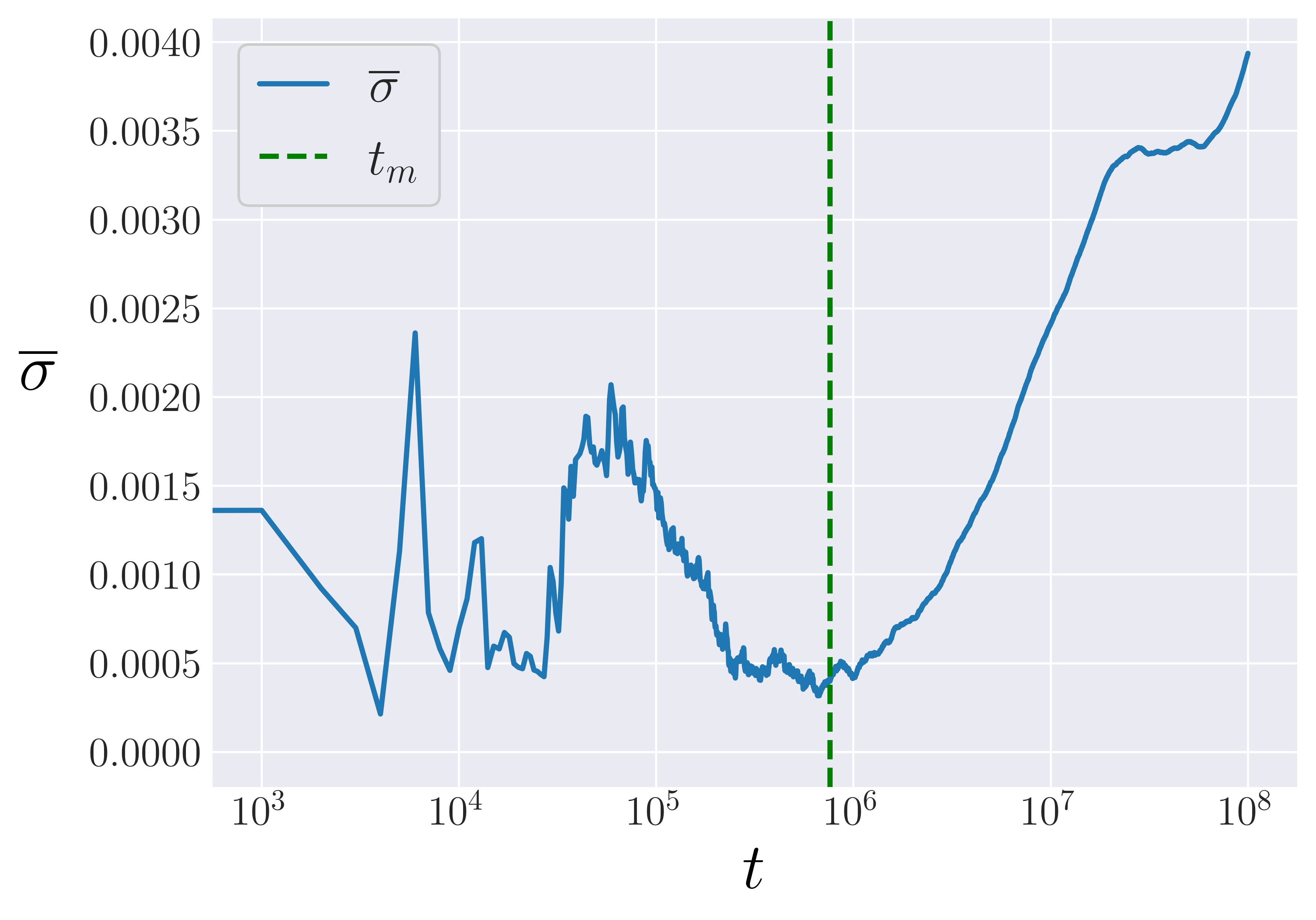
Classical statistical mechanics has long relied on assumptions such as the equipartition theorem to understand the behavior of the complicated systems of many particles. The successes of this approach are well known, but there are also many well-known issues with classical theories. For some of these, the introduction of quantum mechanics is necessary, e.g., the ultraviolet catastrophe. However, more recently, the validity of assumptions such as the equipartition of energy in classical systems was called into question. For instance, a detailed analysis of a simplified model for blackbody radiation was apparently able to deduce the Stefan–Boltzmann law using purely classical statistical mechanics. This novel approach involved a careful analysis of a “metastable” state which greatly delays the approach to equilibrium. In this paper, we perform a broad analysis of such a metastable state in the classical Fermi–Pasta–Ulam–Tsingou (FPUT) models. We treat both the $\alpha$-FPUT and $\beta$-FPUT models, exploring both quantitative and qualitative behavior. After introducing the models, we validate our methodology by reproducing the well-known FPUT recurrences in both models and confirming earlier results on how the strength of the recurrences depends on a single system parameter. We establish that the metastable state in the FPUT models can be defined by using a single degree-of-freedom measure—the spectral entropy ($\eta$)—and show that this measure has the power to quantify the distance from equipartition. For the $\alpha$-FPUT model, a comparison to the integrable Toda lattice allows us to define rather clearly the lifetime of the metastable state for the standard initial conditions. We next devise a method to measure the lifetime of the metastable state $t_m$ in the $\alpha$-FPUT model that reduces the sensitivity to the exact initial conditions. Our procedure involves averaging over random initial phases in the plane of initial conditions, the $P_1$-$Q_1$ plane. Applying this procedure gives us a power-law scaling for $t_m$, with the important result that the power laws for different system sizes collapse down to the same exponent as $E\alpha^2\rightarrow0$. We examine the energy spectrum $E(k)$ over time in the $\alpha$-FPUT model and again compare the results to those of the Toda model. This analysis tentatively supports a method for an irreversible energy dissipation process suggested by Onorato et al.: four-wave and six-wave resonances as described by the “wave turbulence” theory. We next apply a similar approach to the $\beta$-FPUT model. Here, we explore in particular the different behavior for the two different signs of $\beta$. Finally, we describe a procedure for calculating $t_m$ in the $\beta$-FPUT model, a very different task than for the $\alpha$-FPUT model, because the $\beta$-FPUT model is not a truncation of an integrable nonlinear model.

Written using Mathematica, ElectroDynamics is designed as an interactive standalone work aimed at the advanced undergraduate. The power of symbolic manipulation is used to calculate fields from common source distributions that are beyond the scope of a traditional text—for example, the exact magnetic field from a common bar magnet. Executable code is written in a style that is instantly readable because it mirrors traditional formulas. Numerical calculations feature an automatic check of units. Color vector 3D graphics are used liberally to visualize results. The set of nine notebooks covers statics, fields in materials, boundary value problems, conservation laws, waves and waveguides, potentials and fields of moving charges, radiation from a variety of source geometries, and relativistic transformation of potentials, forces and fields. There is enough material for a two-semester course. No prior knowledge of Mathematica is required.

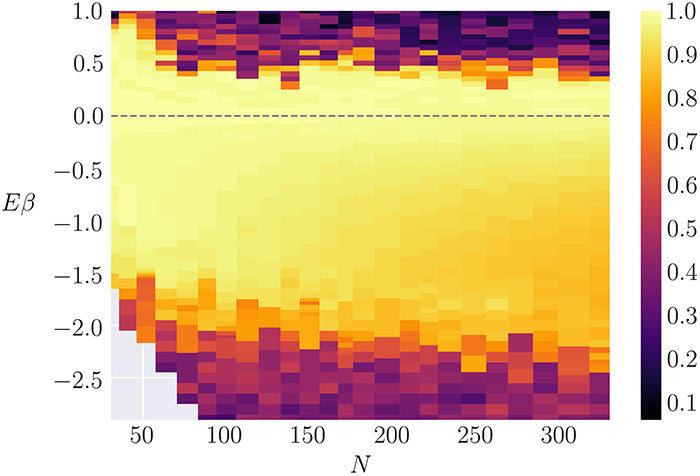
We perform a thorough investigation of the first Fermi-Pasta-Ulam-Tsingou (FPUT) recurrence in the $\beta$-FPUT chain for both positive and negative $\beta$. We show numerically that the rescaled FPUT recurrence time $T_r=t_r/(N+1)^3$ depends, for large N, only on the parameter $S\equiv E\beta(N+1)$. Our numerics also reveal that for small $|S|$, $T_r$ is linear in $S$ with positive slope for both positive and negative $\beta$. For large $|S|$, $T_r$ is proportional to $|S|^{-1/2}$ for both positive and negative $\beta$ but with different multiplicative constants. We numerically study the continuum limit and find that the recurrence time closely follows the $|S|^{-1/2}$ scaling and can be interpreted in terms of solitons, as in the case of the KdV equation for the $\alpha$ chain. The difference in the multiplicative factors between positive and negative $\beta$ arises from soliton-kink interactions that exist only in the negative $\beta$ case. We complement our numerical results with analytical considerations in the nearly linear regime (small $|S|$) and in the highly nonlinear regime (large $|S|$). For the former, we extend previous results using a shifted-frequency perturbation theory and find a closed form for $T_r$ that depends only on S. In the latter regime, we show that $T_r\propto|S|^{-1/2}$ is predicted by the soliton theory in the continuum limit. We then investigate the existence of the FPUT recurrences and show that their disappearance surprisingly depends only on $E\beta$ for large $N$, not $S$. Finally, we end by discussing the striking differences in the amount of energy mixing between positive and negative $\beta$ and offer some remarks on the thermodynamic limit.